堆排序

堆排序（heap sort）是选择排序的一种，不要被它的名字吓到了，堆只是一种数据结构，这个数据结构来自二叉树，准确的说是完全二叉树，完全二叉树就是所有的除最后一层外，其他的层都是满的，不能有空缺，像下面这样。

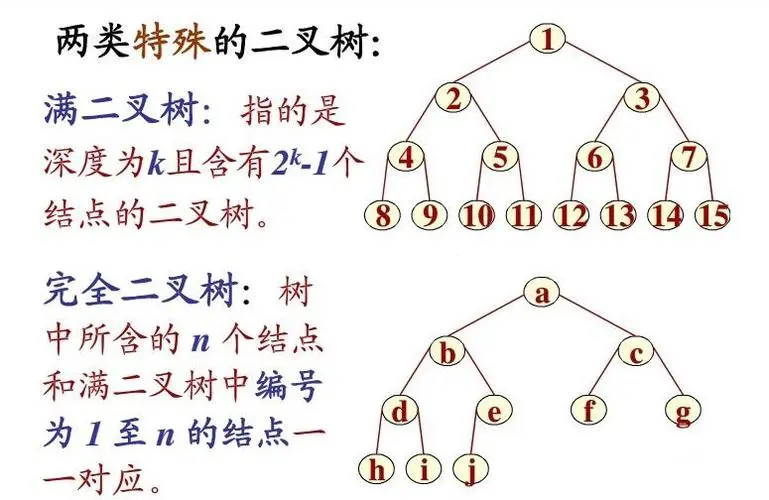
每个节点加上左右的两个元素我们叫做堆，堆分为大顶堆和小顶堆。

大顶堆是值节点元素的值会大于左右节点的值，在整个完全二叉树上都要满足这个条件，小顶堆反之。

思路

我们在给数组排序时并不会真正的去创建一个完全二叉树，这样的话成本太高了，聪明的前辈们发现，数组下标和完全二叉树有一种天然的对应关系，比如就以上图的二叉树为例[a, b, c, d, e, f, g, h, i, j],如果仔细的话就会发现这就是二叉树层序遍历的结果，而且更神奇的是左右节点的下标和他们的父元素有规律，就以a, b, c这三个字符为例吧！我们发现a的下标是0,b的下标是1，c的下标是2，(0 * 2 + 1)=1,(0 * 2 + 2)=2,这不就是当前节点左右子节点下标吗？我们再试一下d这个节点，他的下标是3由上面的规律我们可以得知它的左节点下标为3 * 2 + 1 为 7，在数组中对应h,右下标为3 * 2 + 2为8对应i,所以我们可以得出下面这样一个结论：

我们使用下标来模拟堆时，当前下标所对应的左节点的下标为 i * *2 + 1,右节点为 i * 2 + 2,反之当前节点对应的父节点下标为(i - 1) / 2 。

现在我们可以使用这个规律来构建大顶堆，之后把大顶堆的堆顶，也就是数组的第一个元素和最后一个元素交换，交换之后堆会失去平衡，需要平衡堆之后再重复上述操作，直到数组有序。

代码

import { swap } from "../util/index.mjs";

/**
 * @description 自上而下的构建堆
 * @param {number[]} arr - 需要变成堆结构的数组
 */
function insertHeap(arr) {
  let n = arr.length;
  for (let i = 1; i < n; i++) {
    let cur = i;
    let parent = (i - 1) >> 1;
    while (cur >= 1 && arr[parent] < arr[cur]) {
      swap(arr, parent, cur);
      cur = parent;
      parent = (cur - 1) >> 1;
    }
  }
}

/**
 * @description 交换首尾元素之后纠正堆
 * @param {number[]} arr - 需要纠正的堆
 * @param {number} cur - 从此位置开始纠正
 * @param {number} end - 堆的结束下标
 * @returns 
 */
function correctHeap(arr, cur, end) {
  while (cur * 2 + 1 <= end) {
    // 至少有一个左孩子
    let left = cur * 2 + 1;
    let right = cur * 2 + 2;
    let max;
    if (right <= end && arr[left] < arr[right]) {
      max = right;
    } else {
      max = left;
    }
    if (arr[cur] >= arr[max]) return;
    swap(arr, cur, max);
    cur = max;
  }
}

/**
 * @description 自上而下的堆排序
 * @param {number[]} arr - 需要堆排序的数组 
 */
export function heapSort(arr) {
  insertHeap(arr); // 构建堆
  let end = arr.length - 1; // 数组结束下标
  while (end >= 1) {
    swap(arr, 0, end);
    end--;
    correctHeap(arr, 0, end); // 纠正堆
  }
}

/**
 * @description 自下而上的堆排序
 * @param {*} arr - 需要堆排序的数组
 */
export function heapSort2(arr) {
  // 构建堆
  let end = arr.length - 1;
  let cur = (end - 1) >> 1; // 最后一个非叶子节点
  while (cur >= 0) {
    correctHeap(arr, cur, end);
    cur--;
  }
  // 纠正堆
  while (end >= 1) {
    swap(arr, 0, end);
    end--;
    correctHeap(arr, 0, end); // 纠正堆
  }
}

总结

堆排序是一种特殊的选择排序，每次选择堆顶的元素，如果是大顶堆，那么堆顶的元素就是最大值，如果是小顶堆，那么堆顶的元素就是最小值，我们把堆顶元素和最后一个元素作交换，交换之后把这个元素去掉，由于交换之后堆会失去平衡，我们需要平衡堆（无序重新构建，构建成本太高），平衡之后往复以上操作就可使整个数组有序，大顶堆的方式是正序的，小顶堆是逆序的，可以参考选择排序。