快速排序

快速排序一听这个名字就知道非常的快，那么快速排序是怎么个快法，想必大家都不是太清楚，如果我跟你说快速排序是一种冒泡排序你信吗？就像希尔排序是插入排序的改进版本，堆排序是选择排序的改进版本，快速排序也是冒泡排序的一种改进版本，而且还是暴改。

思路

快速排序的核心思路是选取数组中的一个值作为 pivot(中轴) 小于这个值的元素放到数组的左边，大于这个值的元素放到数组的右边，这个时候递归的处理下标0到pivot-1的子数组和pivot+1到length-1的右边数组，直到递归结束，这个时候数组就是有序的了，说着简单，处理起来是非常麻烦的，首先我们要知道怎么分才能使小于 pivot 的值全部到pivot的左边去，大于pivot的值到右边去，这里大致分为三种做法，分别是左右指针法、挖坑法（这个比较好理解）、前后指针法（抽象难理解），由于快速排序非常的重要，下面我一一讲解这三种主要方法。

左右指针法

假设我们要处理下面这样一个数组 [5, 1. 9, 2, 7, 8, 3, 4, 6]，我们首先创建两个指针left、right，分别指向数组的最左边元素和数组最右边的元素，同时创建一个pivot指向数组的最后一个元素（最前面也可以，处理顺序会有不同），在这个数组中left最初指向5，right最初指向6，pivot也指向6 。首先left不停的往右边找大于pivot的值,right不停的往左找小于pivot的值，找到之后交换left和right对应的值，在第一次寻找中left找到的第一个比pivot大的值为9，right找到的第一个比pivot小的值是4，交换之后原数组会变成[5, 1, 4, 2, 7, 8, 3, 9, 6],这个时候left指向的是4，right指向的是9,由于交换之后当前left和right都不满足寻找的要求所以left会继续往右边找，right会继续往左边找，这个时候left会找到7，right会找到3，我们继续交换，交换之后的数组为[5, 1, 4, 2, 3, 8, 7, 9, 6],这个时候left指向了3，right指向了7，重复上面的操作，left开始往右边找找到了8，right这个时候也开始往左边找，到8的这个时候发现left也在这里，而且left左边的所有数都是right要找的，但是这个时候我们要停止寻找，因为left左边的数都小于pivot，left右边的数都大于pivot，除了数组最后一个元素pivot，这个时候我们只需交换left和pivot的值就能保证pivot左边的值都小于等于pivot，右边的值都大于等于pivot，交换之后的数组为[5, 1, 4, 2, 3, 6, 7, 9, 8]之后我们递归处理即可，参考下面的动画，思路会很清晰，再不明白原理之前不要看代码，不然会非常乱！

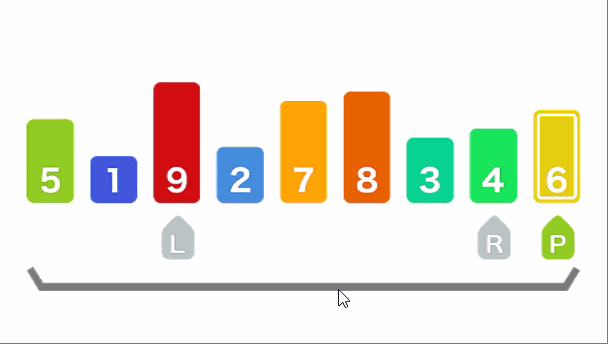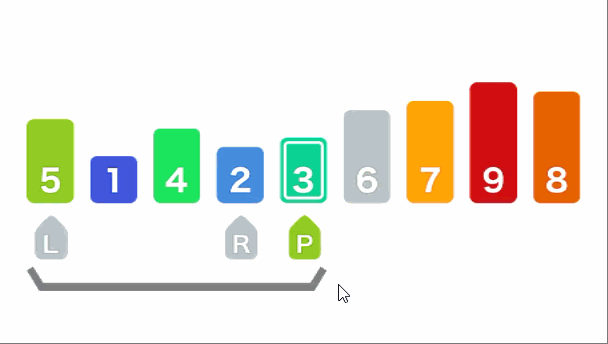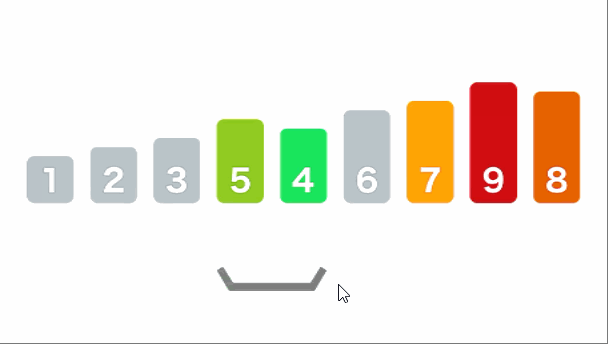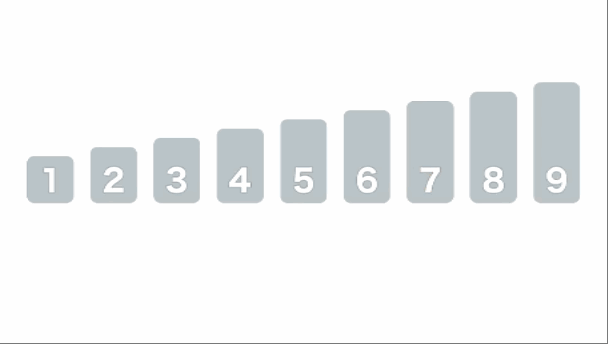
左右指针法代码

import { swap } from '../util/index.mjs';

/**
 *
 * @param {number[]} array - 需要排序的数组
 */
export function quickSort(array) {
  function QuickSort(arr, left, right) {
    if (left < right) {
      const index = partition(arr, left, right); // 左右指针交换元素的函数单独抽取出来
      QuickSort(arr, left, index - 1); // index为pivot无需参与排序
      QuickSort(arr, index + 1, right);// 右半部分同理
    }
  }
  QuickSort(array, 0, array.length - 1);
  return array;
}

/**
 * @description 使用左右指针法来分数组
 * @param {number[]} arr - 需要分治的函数
 * @param {number} left - 开始的位置
 * @param {number} right - 结束的位置
 */
function partition(arr, left, right) {
  const pivot = arr[right]; // 以right作为pivot
  const pivotIndex = right;

  while (left < right) { 
    // left开始往右边找比pivot大的值
    while (left < right && arr[left] <= pivot) {
      left++;
    }
    // right开始往左边找比pivot小的值
    while (left < right && arr[right] >= pivot) {
      right--;
    }
    swap(arr, left, right);
  }
  swap(arr, left, pivotIndex);
  return left;
}

这个方法是最广为流传的一种做法，有没有改进交换左右指针和冒泡排序很像，只是这个过程跨度很大，这也是为什么比冒泡快的原因。

挖坑法

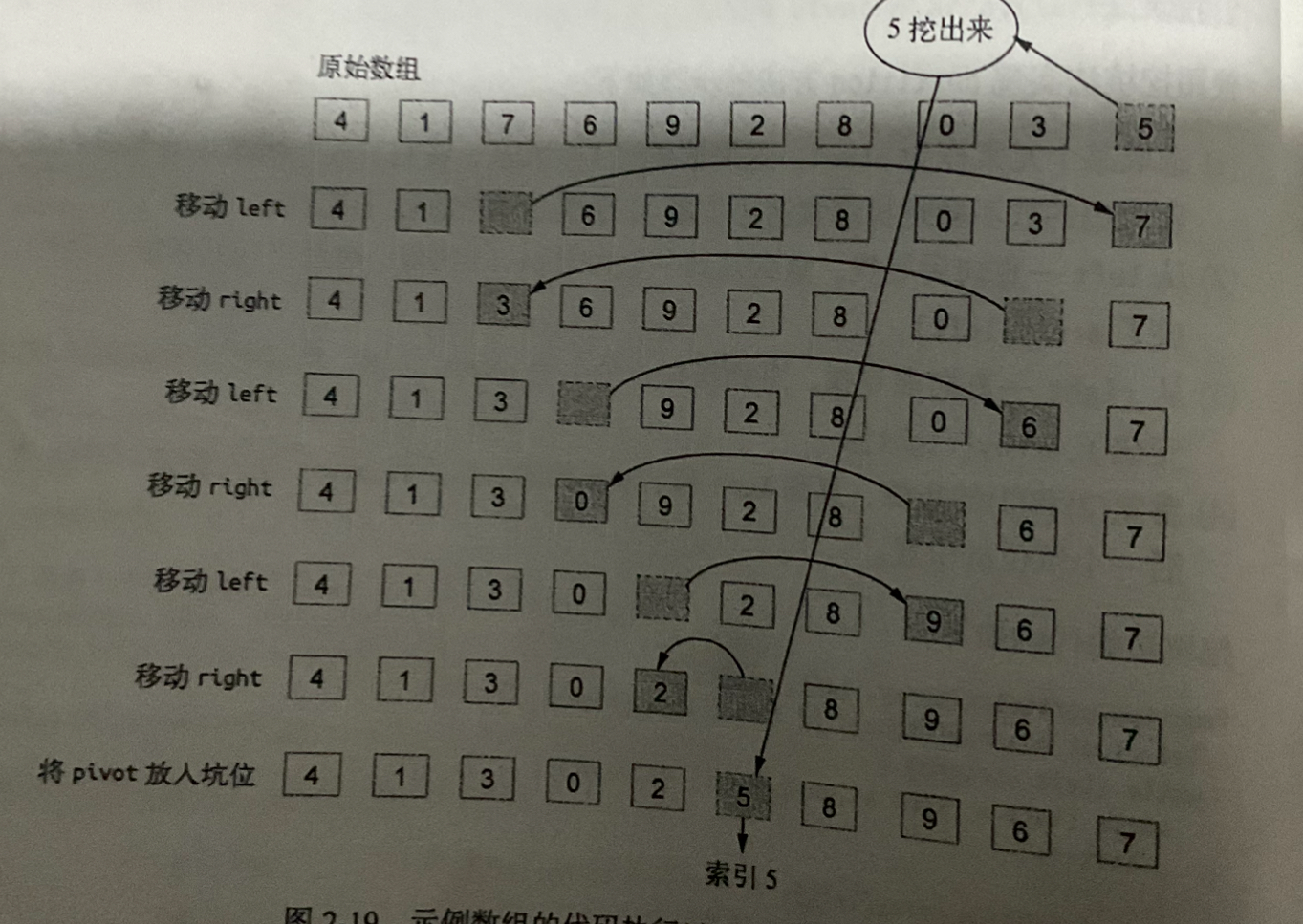
设置三个变量，left、right、pivot 。left指向第一个元素，right指向最后一个元素，pivot保存最后一个元素作为pivot的值，并且假设right这个位置是一个坑，这个时候left开始找比pivot大的值，找到了7，并且把7复制给arr[right]，这个时候数组会出现两个7一个由left指向，一个由right指向，但是left这个指向的是多余的，是一个坑位，这个时候right开始往左边找小于pivot的值，找到了3，arr[left] = arr[right]把这个位置填上，这个时候ight的位置变成了坑位，然后左右交替填坑，直到left不再小于right，我们把最初保存的这个pivot值赋值给left的位置arr[left] = arr[pivot]，这样整个数组就变成左边小于pivot右边大于pivot，之后再递归处理剩余的部分。

挖坑法代码

/**
 *
 * @param {number[]} array - 需要快速排序的数组
 */
export function quickSort2(array) {
  function QuickSort(arr, left, right) {
    if (left < right) {
      const pivot = partition2(arr, left, right);
      QuickSort(arr, left, pivot - 1);
      QuickSort(arr, pivot + 1, right);
    }
  }
  QuickSort(array, 0, array.length - 1);
}

/**
 * @description 使用挖坑法来分数组
 * @param {number[]} arr - 需要分解的数组
 * @param {number} left - 开始的位置
 * @param {number} right - 结束的位置
 */
function partition2(arr, left, right) {
  const pivot = arr[right];
  while (left < right) {
    while (left < right && arr[left] <= pivot) {
      left++;
    }
    arr[right] = arr[left];
    while (left < right && arr[right] >= pivot) {
      right--;
    }
    arr[left] = arr[right];
  }
  arr[left] = pivot;
  return left;
}

挖坑法和之前的左右指针法最大的区别就是不用交换元素，通过不停的挖坑，填坑的方式找到pivot合适的位置，直到把pivot放进去即可，理解起来比较容易。

前后指针法

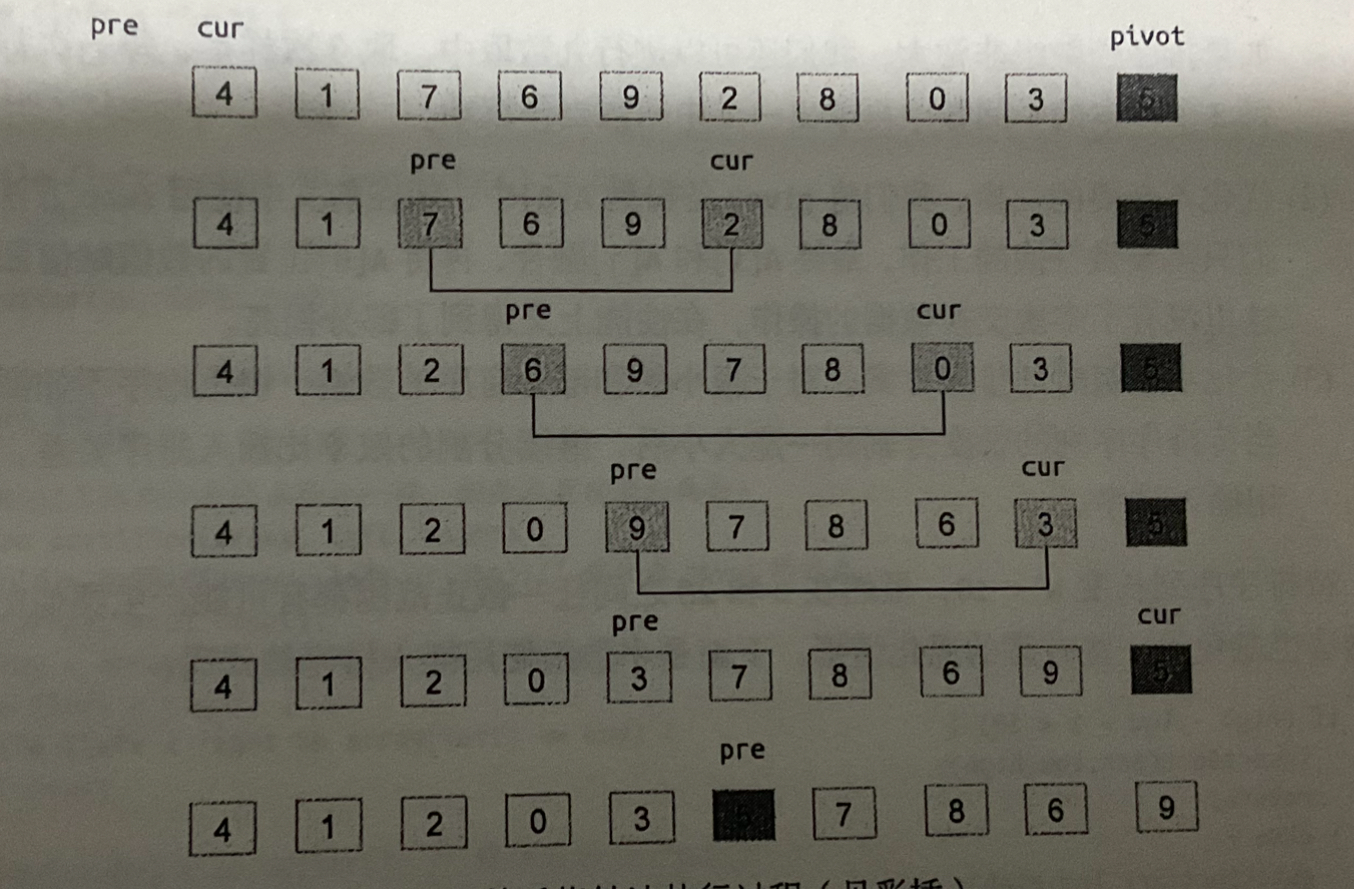
我们定义两个指针一个pre一个cur，pre最初指向cur的前一个元素，cur最初指向第一个元素，同样按照老规矩以最后一个元素作为pivot(不要问我为什么，我喜欢从左往右开始找)。cur最初为0,pre为-1，cur往后面开始找小于pivot的值，如果找到就把pre++之后再与之交换（是不是一头雾水，why，别急），我们看上面的图会发现，第一次cur找到了4然后pre加1也指向了4，自己和自己交换等于没交换，我们继续往下看，cur继续往下面找到了1,这个时候pre加1也指向了1自己和自己交换等于没交换，，之后cur一直往下找,发现7不是自己要找的，6也不是，直到找到2,这个时候pre加一后指向了7并与2交换，我们会发现交换之后pre到cur，左开右闭这个区间的所有元素都是大于等于pivot的，之后继续按照这个方法操作我们会发现当cur到达最后一个元素的时候，我们交换cur和(pre+1)，就可以保证pivot左边的值小于pivot，右边的值大于pivot.这么弄虽然麻烦，但是有一个好处，因为我们每次都是往后面+1的找，所以这个方法不仅适合数组，也适合列表。

前后指针法代码

/**
 * @description 使用前后指针法分数组
 * @param {number[]} array - 需要排序的数组
 */
export function quickSort3(array) {
  function QuickSort(arr, left, right) {
    if (left < right) {
      const pivot = partition4(arr, left, right);
      QuickSort(arr, left, pivot - 1);
      QuickSort(arr, pivot + 1, right);
    }
  }
  QuickSort(array, 0, array.length - 1);
}

/**
 * @description 使用前后指针法(优化版)
 * @param {number[]} arr
 * @param {number} left - 开始的位置
 * @param {number} right - 结束的位置
 */
function partition4(arr, left, right) {
  let cur = left;
  let pre = left - 1;
  const pivot = arr[right]; // 选取最后一个元素作为中枢
  while (cur < right) {
    if (arr[cur] < pivot && ++pre !== cur) {
      swap(arr, pre, cur);
    }
    cur++;
  }
  /*
        循环结束之后pre所处的元素之前都是小于pivot（包含pre）,右侧的元素都是大于或等于pivot的，交换cur+1和pviot的值
    */
  swap(arr, pre + 1, right);
  return pre + 1;
}

优化之后的partition

/**
 * @description 使用前后指针法(优化版)
 * @param {number[]} arr
 * @param {number} left - 开始的位置
 * @param {number} right - 结束的位置
 */
function partition4(arr, left, right) {
  let cur = left;
  let pre = left - 1;
  const pivot = arr[right]; // 选取最后一个元素作为中枢
  while (cur < right) {
    if (arr[cur] < pivot && ++pre !== cur) {
      swap(arr, pre, cur);
    }
    cur++;
  }
  /*
        循环结束之后pre所处的元素之前都是小于pivot（包含pre）,右侧的元素都是大于或等于pivot的，交换cur+1和pviot的值
    */
  swap(arr, pre + 1, right);
  return pre + 1;
}

太简短了，而且难理解，建议直接复制粘贴😂。

非递归方式

看完上面的代码会发现一件事，那就是当我们把partition提取出来之后，所有的快速排序写法都是一样的，所以我们只要模拟上面的partion这个过程就能使用非递归的方式排序好数组，递归说到底就是函数栈的调用，先进后出，现在我们使用数组的push和pop来模拟栈不就可以了吗？这太简单了，直接上代码。

/**
 * @description 使用非递归方式实现快速排序
 * @param {number[]} arr - 需要排序的数组
 */
export function quickSort4(arr) {
  if (!arr.length || arr.length === 1) return; // 数组为空，或者数组为1，不处理
  const left = 0;
  const right = arr.length - 1;
  const stack = []; // js的数组有push和pop符合栈结构
  stack.push(right);
  stack.push(left);
  while (stack.length) {
    const l = stack.pop(); // 弹出需要处理的左边l
    const r = stack.pop(); // 弹出需要处理的有边界
    const pivot = partition4(arr, l, r);
    // l < pivot - 1 说明还可以分，当l = pivot -1 说明pivot左侧就一个数，说明左侧已经有序了无须再分
    if (l < pivot - 1) {
      stack.push(pivot - 1);
      stack.push(l);
    }
    if (r > pivot + 1) {
      stack.push(r);
      stack.push(pivot + 1);
    }
  }
}

总结

快速排序的效率非常的高，在数据量大的时候直接拉开一众算法，所以是面试的重灾区，一定要会快速排序，就像每个人都会冒泡排序一样，同时也要知道快速排序的核心partition，这是快速排序最重要的一部分，完全可以作为单独的逻辑，所以与其说是快速排序还不如叫"左小右大排序" 。partition有三种主要思想分别是左右指针法、挖坑法、前后指针法，最后一种前后指针法非常难以理解，但是只有它能给链表排序，所以也一定要学会，不懂也没关系，多看几遍，多想想就会了。