gcd(辗转相除法)证明

辗转相除法

如何求两个数的最大公约数大部分人想到的方式就是 辗转相除法，也叫 欧几里得算法，但是我是一个有强迫症的人，我想知其然，更想只其所以然。辗转相除法的代码非常简单，如下：

function gcd(a, b) {
  return a % b === 0 ? b : gcd(b, a % b);
}

假设 a = 15, b = 6 在计算时先求 a % b == 3, 之后再求 6 % 3 == 0 当模的结果为0时这个 3 就是最大公约数；Why?

证明

传统的证明方式属实难以理解，对我来说没有说服力，这里我用几何的方式证明，证明方式很简单，小学生经常考的一种题目就是，在一个长方形的地面上贴正方形瓷砖，当正方形的边长为多少时，使用的正方形数量最少，假设长方形地面的长为a,宽为b，那么这个边长c不就是最大公约数嘛！这个抽象过程应该不难理解，因为c就是a和b的公共最大因子，这也是最大公约数的定义。

1. 画任意（矩形）：

画任意一个矩形，我这里以长为15，宽为6的长方形为例：

2.用宽来分割

首先我们可以肯定的是任何两个正整数都有公约数，即使它们都是质数，也有公约数 1 ，抽象成几何就是任何一个矩形都能分割成任意大小的正方形，如果长刚好是宽的倍数，那么这个矩形刚好可以分割成以宽为边长的任意个正方形，此时宽就是最大公约数，这和代码的判断条件一致return a % b === 0 ? b, 假设a=12、b=6 那么就会返回6。

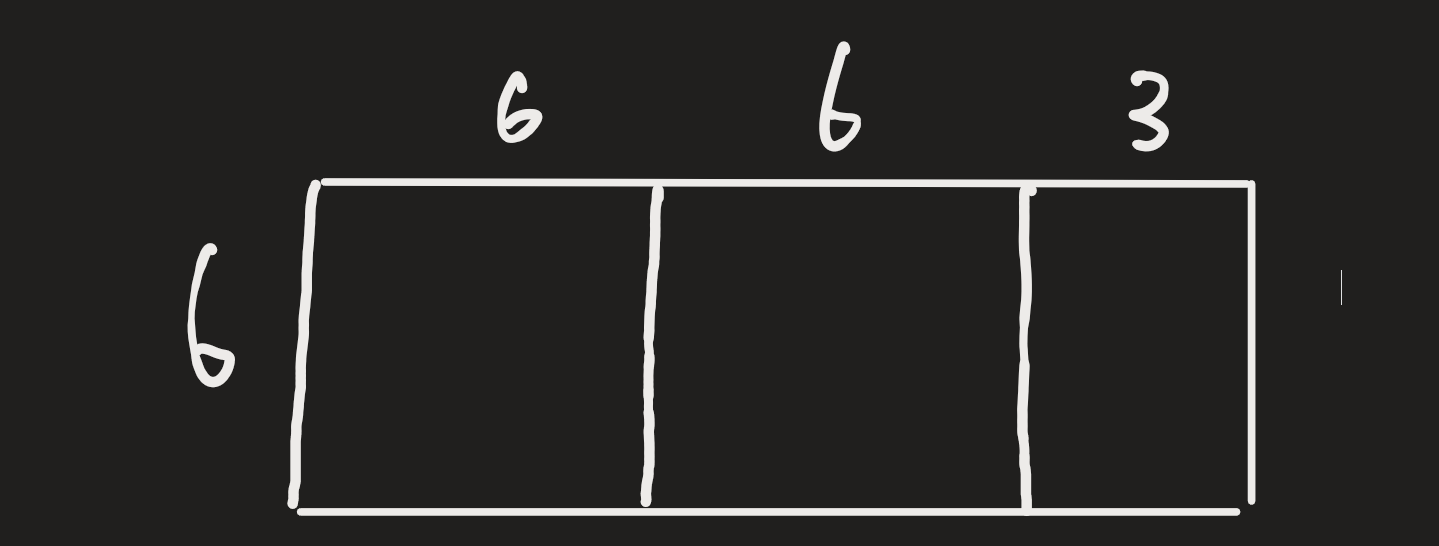
3.继续分割剩余的小矩形

遗憾的是，用宽：6，来分割长：15，最后剩下了一个小矩形，这个小矩形的长为之前矩形的宽，而宽则是，长mod6的余数，根据公约数的定义，小矩形的公约数一定能被自己的长和宽整除，而小矩形的长正好是大矩形的宽，而大矩形已经被分割成了边长为小矩形长的矩形，所以，以小矩形公约数为边长的正方形刚好可以分割大矩形分割下来正方形，也就是说如果大矩形的宽不能作为分割的最大正方形边长，只要剩下的那个小矩形能被分割成任意个小正方形那么这个小正方形也能分割大正方形，那么它就能分割整个大矩形，那么它的边长就是最大公约数。

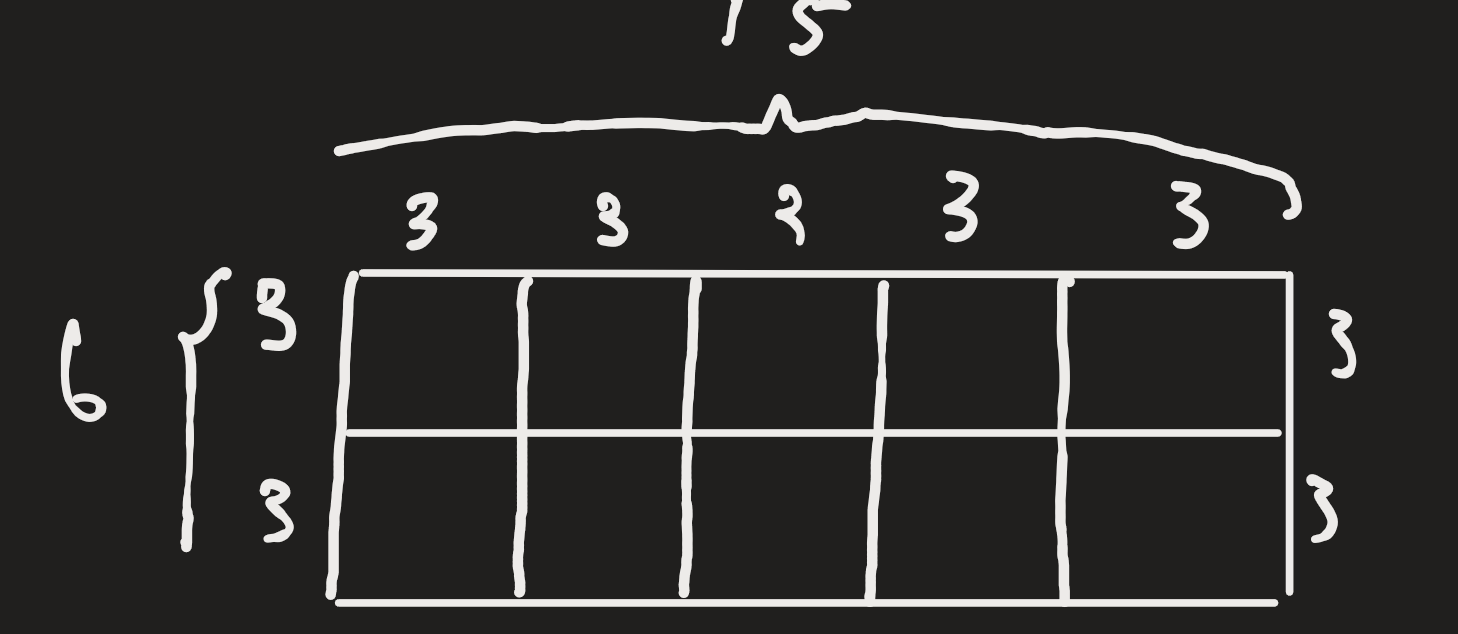
这个图没怎么画好，但是大致意思明白就可以了，所以辗转相除的几何意义就是：用宽来分割正方形，如果分割完之后还剩下一个矩形，那么继续用剩下的矩形的宽来分割，如果还是不能完整分割，那么就用剩下矩形分割之后剩下的矩形的宽继续分割，直到能完整分割为止。 这个分割下来的正方形一定能填充初始的矩形，因为初始矩形的宽是小矩形的长。在来看看完整代码就一目了然了。

function gcd(a, b) {
  // 如果长能被宽整除那么宽就是最大公约数，如果不能，就把宽作为长，余数作为宽继续调用，直到能整除为止
  return a % b === 0 ? b : gcd(b, a % b);
}

小结

辗转相除的几何本质就是：能填充剩余矩形的正方形，也一定能填充大矩形，之所以能保证是最大公约数是因为，每一次都默认宽为最大公约数，根据最大公约数的定义，最大公约数不可能比 Math.min(a,b)大，所以一定能保证求出的值是最大公约数。 这个过程画画图就明白了。

lcm最小公倍数

知道如何求最大公约数，最小公倍数非常好求，这里作一下简单的证明即可。

证明： 还是以上面求最大公约数的两个数字为例，假设我们有两个数字15和6，通过上面的辗转相除法证明可知，它的gcd为3，也就是说它们的最大公共因子就是3，也就是说15包含两个因子3和5,6包含两个因子2和3,把这两个数相乘，再除以它的公共因子能保证这个数一定是这两个数的公倍数，而这个公共因子又是最大的，所以lcm等于两数之积与两数gcd的商（a*b/gcd(a,b))。

求第N个神奇的数字

这个题目叫我们求第n个神奇的数字，根据神奇数字的描述，它们一定对有重合的部分，这里会用到最小公倍数，具体描述 👉leetcode878

function nthMagicalNumber(n, a, b) {
    // 计算 a 和 b 的最小公倍数
    const lcm_ab = (a * b) / gcd(a, b);
    
    // 计算小于等于 x 的魔法数字个数
    function count(x) {
        return Math.floor(x / a) + Math.floor(x / b) - Math.floor(x / lcm_ab); // 所有的魔法数字减去公共的魔法数字
    }
    
    // 二分查找
    let left = 1, right = Math.min(a, b) * n;
    const MOD = 1e9 + 7;
    
    while (left < right) {
        let mid = Math.floor((left + right) / 2);
        if (count(mid) < n) {
            left = mid + 1;
        } else {
            right = mid;
        }
    }
    
    return left % MOD;
}

// 计算最大公约数
function gcd(x, y) {
    while (y !== 0) {
        let temp = y;
        y = x % y;
        x = temp;
    }
    return x;
}

总结

这篇文章从几何的角度证明了为什么辗转相除法可以求最大公约数，几何的角度更加直观更有说服力，一旦理解很难遗忘，并解释了最小公倍数lcm和最大公约数gcd之间的关系，并利用最小公倍数来出去除重复的神奇数字，重点理解辗转相除法的原理就行。