KMP算法核心思想理解
简介
KMP是一个高效的字符串子串匹配算法,高效的原因在于它不会和暴力匹配算法那样对每一个可能的子串去进行比较,而是会通过 模式串 中已经匹配的那一部分的公共前后缀来快速越过不可能匹配的部分,这样就可以快速匹配到目标子串,如果匹配串的长度为n,模式串的长度为m,那么使用暴力算法需要遍历前 n-m 个字符,并且从当前位置开始遍历模式串的m个字符,比较模式串的字符是否和匹配串中的字符完全相等,所以暴力算法的复杂度是O(n*m), 在匹配串和模式串较大的情况下,这个算法效率极低,而KMP算法是严格的O(n+m),从后面的分析中你就会明白。
匹配过程
很多人在讲kmp的时候总是先介绍Next数组,然后就教你Next数组怎么用,然后就实现了算法,这样看完,很多人就会在没理解的情况下记住了kmp的代码片段,压根就没理解,我当初也是这样的,我认为这种教学是错误的,正确的过程是告诉学者 KMP 的匹配过程,而这个匹配过程需要用到 Next数组 这个 Next数组 我待会会讲,现在我们来思考匹配过程。
假设我们有匹配串: ABACABAFABACABAE, 模式串:ABACABAE,首先我们需要挨个比较:
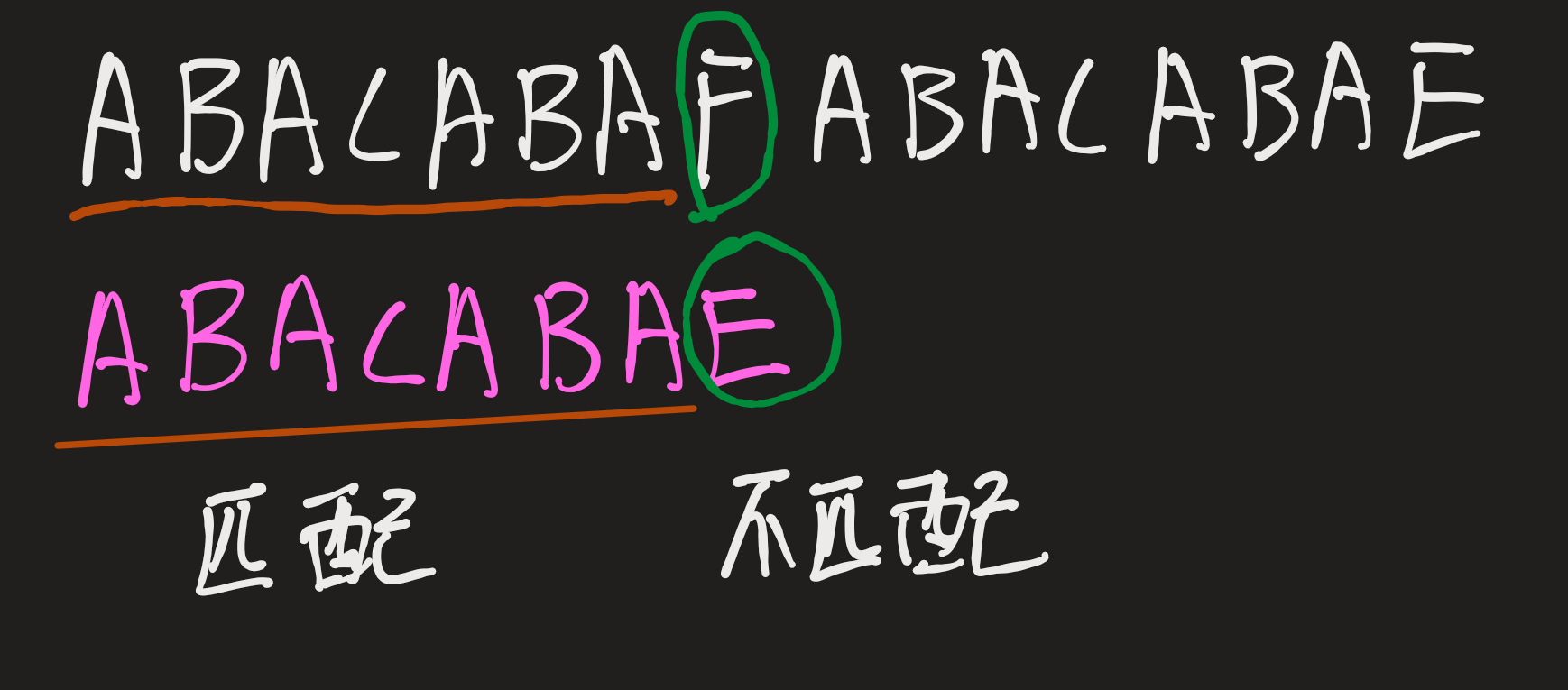
通过上面的图片我们可以发现,现在红线所标记的部分已经是匹配的,但是绿圈标记的这个字符没有匹配,先来看看红色下划线的部分ABACABA,这个字符串有一个特点,他的前面的三个字符和后面的三个字符是相等的,那我能按照 ABA 这个 模式串 的头部匹配吗?如果可以它会漏掉可能的开头吗?我的答案是可以,而且不会溜掉任何的可能。证明我会放在后面,现在只看匹配过程。

现在我们不是按照暴力算法的一个字符一个字符的移动,而是按照ABA,从匹配串的第一个ABA跳到下一个ABA,在这个时候我们发现ABA后面的那个字符还是没有匹配,此时模式串中的匹配部分由之前的ABACABA变成了ABA,这个时候只能按照A来移动,从第一个A移动到第二个A.

这个时候还是不匹配,但这个时候已经没有像之前那样前面和后面一致的字符子串了,所以我们直接重新从F位置匹配整个模式串。

还是不匹配,这样的话就从匹配串的下一个字符比较。
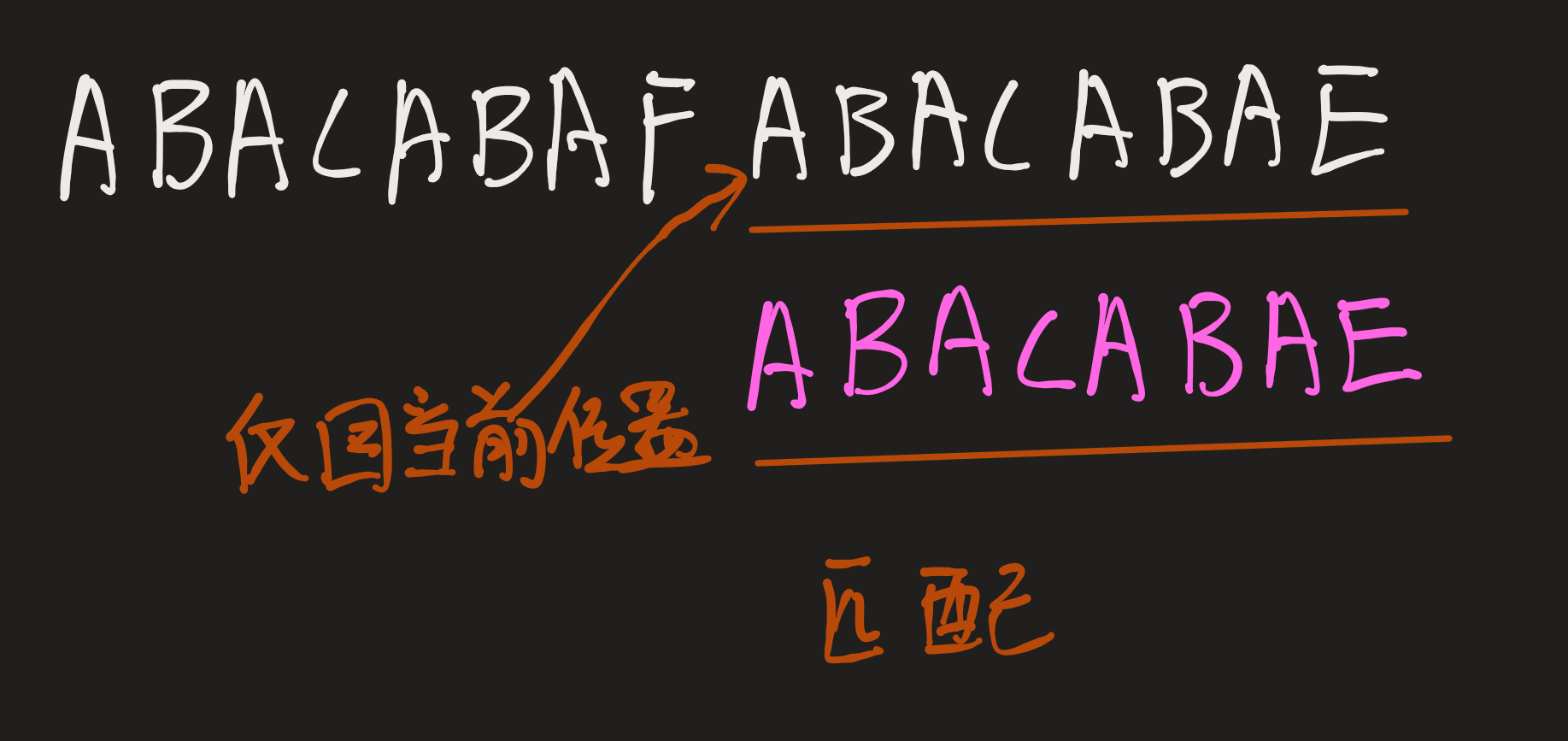
最后匹配完成,返回A的位置就是这个模式串在匹配串中出现的位置。
思考
证明 "从第一个ABA跳到第二个ABA,中间会不会出现匹配整个 模式串 的开头部分!
这是不可能的,因为这两个ABA已经在整个匹配的部分ABACABA中,如果中间出现能匹配整个模式串,会发生下面这种情况,第二个ABA的前面任意多个字符和ABA组成的新字符串,是已经匹配字符串的开头一部分,并且它比ABA更长,假设它是四个字符,按照假设他一定会存在,但是只要我们保证ABA是这种可能的最长字符串,那么这个假设不成立,也就是说你只要保证ABACABA 的前面部分从第一个字符开始数的任意多个字符串(前缀),和后面部分从中间开始数,以最后一个字符结尾的任意长字符(后缀),只要保证它们相等,而且最长,那么前缀和后缀的中间位置不可能出现完整匹配模式串的开头,换句话说,只要保证前缀和和后缀相同,而且是最长的,就能保证中间的所有字符位置不可能作为模式串在匹配串中的开始位置! 你可以自己随便举例,比如:匹配串,bcb ***** bcb,模式串bcbabab 在****中你可以填入任意个字符,只要保证前缀和后缀 bcb是最长的,那么绝对不会出现 **bcb是模式串bcbabab开头部分,那么从 ** 这个位置也不可能匹配完整的模式串bababab,仔细理解这个过程,这个过程没有理解清楚,就很难理解KMP的核心原理。
next数组
next数组 的作用非常简单,就是告诉你,如果发生了不匹配,那么指向不匹配位置的指针,跳转到什么位置继续匹配。
我们遍历整个模式串,用 i 表示后缀的最后一个字符,j 表示前缀的最后一个字符, 使 i 初始化为0, j 初始化为1,因为根据前后缀的定义,前缀的开头和后缀的开头不能是同一个位置,如果相等则j++,并且使next[i] = j,如果不相等,使j=next[j-1] 看有没有更短的后缀,由于j-1所以还要保证j>0,直接上代码
// 1. 如果想使用kmp来快速跳过无用的遍历,就需要计算出模式串needle的next数组
const next = new Array(m).fill(0); // 初始化所有位置的前缀值为0(值初始化第一个位置也行)
for (let i = 1, j = 0; i < m; i++) { // i指向后缀的最后一个字符,j指向前缀的最后一个字符,按照kmp对前缀的定义,i初始化为1,j初始化为0
// 如果不相等,表示i指向的这个后缀最后一个字符和j指向前缀的最后一个字符不相等,这个时候我们需要找next[j-1]这个位置的字符
// 是否等于i指向的这个字符,以abaabaf为例,假设现在j指向abaa,i指向abaf,由于j和i指向的字符不相等,所以按照要求j应该移动
// next[j-1]的位置,j-1指向的是aba,next[j-1]表示的就是最大公共前后缀的长度那就是前缀”a“和后缀”a“长度为1,所以j指向了1,
// j=1时 指向的b并不等于f,所以还要继续把j移动到当前位置的next[j-1],所以这是一个循环的过程,并且要保证j>0,不然就会出现越界错误
// 上面的描述可能有点模糊可能体现不出为什么需要把j移动到next[j-1]的位置,
// abaabaf j = 3, i = 6, 前缀abaa 后缀abaf,显然不相等 所以后缀不可能包含aba了,只能aba里面的最大工作前后缀
// abaabaf j = 1, i = 6, 前缀ab,后缀af,显然不相等,继续往前找
while (j > 0 && needle[i] !== needle[j]) {
j = next[j - 1];
}
if (needle[i] === needle[j]) { // 如果相等,表示最大相同前缀需要往后移动一位
j++;
}
// 把当前j表示的就是最大前后缀长度
next[i] = j;
}
KMP实现indexOf
/**
*
* @param {string} haystack 匹配串
* @param {string} needle 模式串
* @return {number} 模式串在匹配串中出现的第一个位置
*/
function indexOf(haystack, needle) {
const n = haystack.length; // 匹配串的长度
const m = needle.length; // 模式串的长度
// 1. 如果想使用kmp来快速跳过无用的遍历,就需要计算出模式串needle的next数组
const next = new Array(m).fill(0); // 初始化所有位置的前缀值为0(值初始化第一个位置也行)
for (let i = 1, j = 0; i < m; i++) { // i指向后缀的最后一个字符,j指向前缀的最后一个字符,按照kmp对前缀的定义,i初始化为1,j初始化为0
// 如果不相等,表示i指向的这个后缀最后一个字符和j指向前缀的最后一个字符不相等,这个时候我们需要找next[j-1]这个位置的字符
// 是否等于i指向的这个字符,以abaabaf为例,假设现在j指向abaa,i指向abaf,由于j和i指向的字符不相等,所以按照要求j应该移动
// next[j-1]的位置,j-1指向的是aba,next[j-1]表示的就是最大公共前后缀的长度那就是前缀”a“和后缀”a“长度为1,所以j指向了1,
// j=1时 指向的b并不等于f,所以还要继续把j移动到当前位置的next[j-1],所以这是一个循环的过程,并且要保证j>0,不然就会出现越界错误
// 上面的描述可能有点模糊可能体现不出为什么需要把j移动到next[j-1]的位置,
// abaabaf j = 3, i = 6, 前缀abaa 后缀abaf,显然不相等 所以后缀不可能包含aba了,只能aba里面的最大工作前后缀
// abaabaf j = 1, i = 6, 前缀ab,后缀af,显然不相等,继续往前找
while (j > 0 && needle[i] !== needle[j]) {
j = next[j - 1];
}
if (needle[i] === needle[j]) { // 如果相等,表示最大相同前缀需要往后移动一位
j++;
}
// 把当前j表示的就是最大前后缀长度
next[i] = j;
}
// 经过上面的计算,我们获得了一个模式串的next数组,现在我们就可以通过这个数组快速匹配了
for (let i = 0, j = 0; i < n; i++) {
// 如果当前字符不匹配,则回溯
while (j > 0 && haystack[i] !== needle[j]) {
j = next[j - 1]; // 回溯到上一个可能的匹配位置
}
// 如果匹配成功,继续检查下一个字符
if (haystack[i] === needle[j]) {
j++;
}
// 如果完整匹配模式串,则返回匹配的起始位置
if (j === m) {
return i - m + 1;
}
}
return -1; // 没有匹配到
}
总结
KMP的核心思想就是通过匹配部分的前后缀信息,把模式串从前缀的开头,移动到后缀的开头,跳过中间不可能的部分,从而提高匹配效率,但是这个移动的过程需要next数组来实现,所以KMP的难点就在实现这个Next数组, 多看一些匹配过程的动画就明白了。


评论区