归并排序

希尔排序给我们带来了一个新思路，将一个问题拆分成几个小规模的子问题，然后用现成的方案解决这些子问题，再慢慢合并问题来解决原问题。归并排序就是采用这种思想的算法。

思路

归并排序会一次性把一个很大的数组分成若干个长度为1的数组，长度为一的数组当然也是有序的，这个时候怎么合并就是解决问题的核心，由于所有的长度为1的数组是有序的，这个时候我们只要把两个长度为1的数组合并成1个长度为2的有序数组，再把两个长度为二的数组合并成1个长度为4的数组，直到两个长度为ｎ／2的数组合并成一个长度为n的数组，这个时候我们就还原了原数组，要想原数组变得有序，只需要在合并的时候做一下比较即可，比如说[1,3],[2,4]这个数组我们可以使用两个指针left和right分别指向第一个数组的1和第二个数组的2，比较left是否小于right如果小于就把left对应的值push到新数组中去，之后left++再比较如果大于就把right对应的值push到数组中去，直到left等于数组长度，或者right等于数组长度，再把剩余的内容全部push到新数组中即可，这个时候合并完成的数组是有序的。

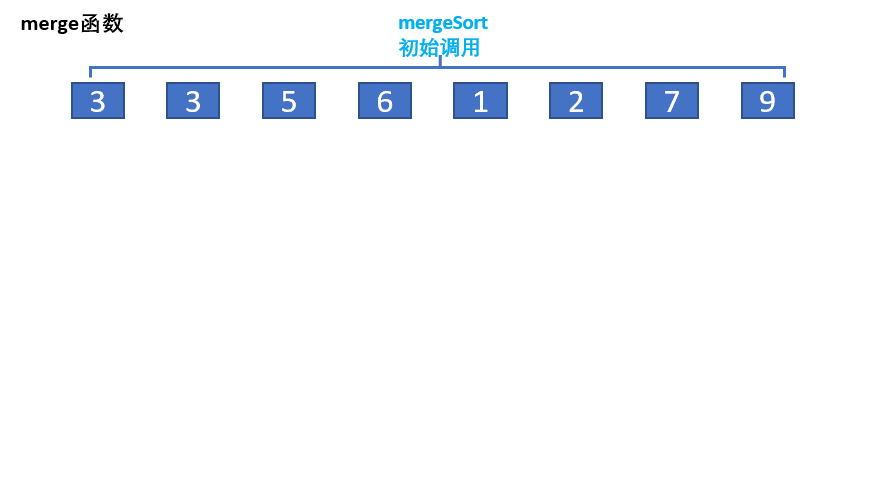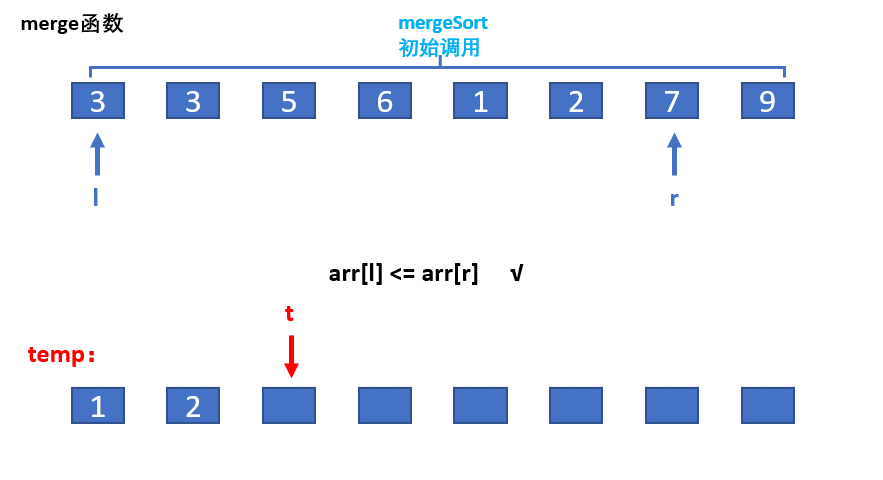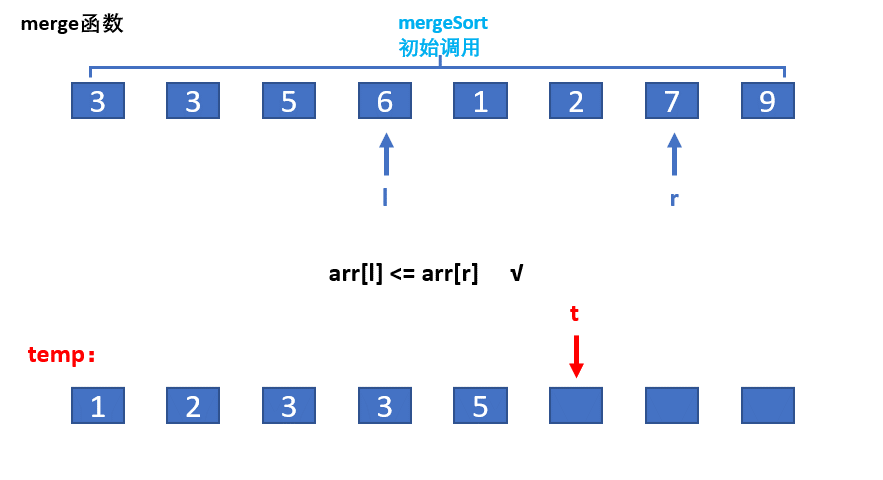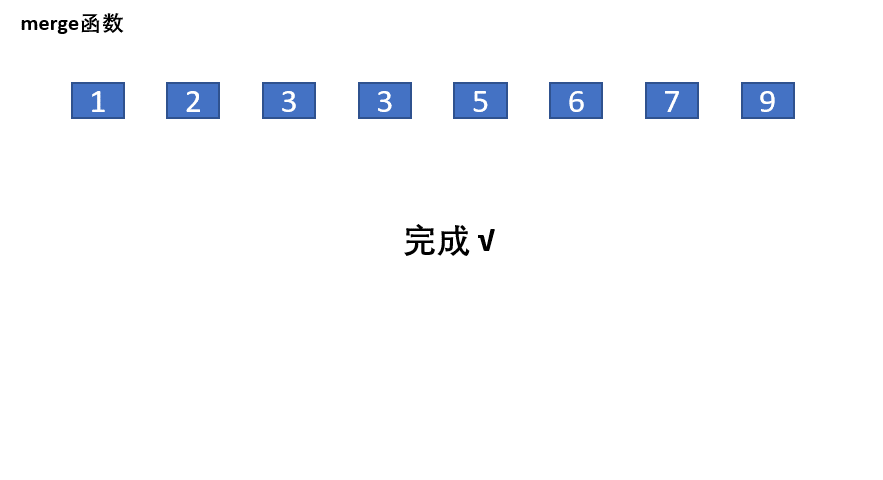
代码

/**
 * @description 不修改原数组，返回新数组
 * @param {number[]} left - 需要合并的左数组
 * @param {number[]} right - 需要合并的右数组
 */
export function mergeSort(arr) {
  if (arr.length <= 1) {
    return arr; // 已经有序
  }

  // 分解
  const middle = Math.floor(arr.length / 2);
  const left = arr.slice(0, middle);
  const right = arr.slice(middle);

  // 递归地对左右两部分进行归并排序
  const sortedLeft = mergeSort(left);
  const sortedRight = mergeSort(right);

  // 合并
  return merge(sortedLeft, sortedRight);
}

function merge(left, right) {
  const result = [];
  let leftIndex = 0;
  let rightIndex = 0;

  // 比较两个数组的元素，将较小的元素加入结果数组
  while (leftIndex < left.length && rightIndex < right.length) {
    if (left[leftIndex] < right[rightIndex]) {
      result.push(left[leftIndex]);
      leftIndex++;
    } else {
      result.push(right[rightIndex]);
      rightIndex++;
    }
  }

  // 将剩余的元素加入结果数组
  return result.concat(left.slice(leftIndex), right.slice(rightIndex));
}

export default mergeSort;

我们可以发现归并排序没有修改元数组，而是返回了一个新的数组，如果想要修改原数组可以遍历新数组把对应的值都插进去，但是这样时间复杂度就上来了，没必要。

总结

归并排序和我们之前的排序有非常大的区别，首先归并排序并没有在原数组中交换变量，而是借用了其他的数组来保存变量，这样会导致归并排序的空间复杂度会明显高于其他的排序，但是空间换时间是值得的。如果你细心的话就会发现，归并排序并没有交换变量的过程，所以就不会存在排完序之后原本相同的两个数之前的跑到后面去，也就是说归并排序是一个O(nlogn)的算法，并且还是一个稳定排序算法，需要考虑稳定性的话可以考虑此算法，像我们熟知的火狐浏览器的Array.prototype.sort()的核心实现就是归并排序，而google使用的是快速排序+冒泡。